Sobre la medición reciente del muón

Foto de Reidar Hahn. Imagen con permiso de Fermilab (en alta resolución aquí).

Gastón Giribet. Facultad de Ciencias Exactas Naturales, Universidad de Buenos Aires y CONICET.

Los muones son partículas fundamentales. Son, en efecto, partículas muy comunes en nuestro entorno. Acaso alcance con decir que un muón atraviesa tu corazón cada segundo. Y al igual que éste, parecen encerrar secretos.

El espín del muón

En la rapsódica clasificación de partículas elementales que damos en llamar Modelo Estándar de la física de partículas, los muones pertenecen a la subfamilia cuyos miembros se denominan “leptones”, entre los que también encontramos al electrón. De hecho, el muón puede ser considerado un hermano mayor del electrón, ya que comparte con éste todas sus propiedades, excepto su masa: Los muones tienen una masa de aproximadamente 105 MeV, lo que los hace unas doscientas veces más masivos que el electrón; pero, más allá de esa diferencia, son exactamente iguales: tienen la misma carga eléctrica que el electrón (e = -1) y tienen el mismo espín que el electrón (s = ½).

El espín, como sabemos, es un grado de libertad que las partículas fundamentales exhiben. El fotón tiene espín s = 1, los leptones tienen espín s = ½, al igual que los quarks, y las otras partículas tienen otros valores del espín, éstos siempre dados por números semi-enteros: los fotones y los gluones, por ejemplo, tienen espín s = 1, al igual que las partículas W y las Z, mientras que la el bosón de Higgs es la única partícula de las 37 que conforman el Modelo Estándar que no presenta espín, i.e. cuyo espín es s = 0.

El espín es, decíamos, un grado de libertad que las partículas presentan. Así como tienen masa, carga eléctrica u otros tipos de carga, las partículas también tienen espín. El espín puede considerarse como una unidad elemental de giro. Al ser las partículas fundamentales puntos en el espacio, el espín de éstas no puede, stricto sensu, ser pensado como el giro de la misma, ya que no hay en ellas un volumen que gire. Cabe recalcar que las partículas elementales no son pequeñas, ni muy pequeñas, ni muy muy pequeñas, sino que son infinitamente pequeñas; son, hasta donde sabemos, puntos en el espacio. Debido a esto, el espín debe ser pensado como una “unidad de giro”, un giro elemental, un giro inmanente de esos puntos en el espacio a los que llamamos partículas, un giro que está antes que aquello que gira. Esto, lo sé, puede resultar conceptualmente escurridizo, pero eso sólo se debe a que nuestro entendimiento, perezoso, insiste con pensar a todo girar como el girar de algo. No ocurre así con las partículas puntuales: El espín es giro, un giro inmanente, no es el girar de algo.

Pero, ¿por qué hablamos tanto del espín? Pues bien, … es que el espín es importante para entender la cuestión que nos convoca. Expliquemos el porqué.

Al ser partículas cargadas eléctricamente y al tener espín, los muones, así como los electrones, presentan un momento magnético. Es decir, podemos pensarlos como pequeños dipolos magnéticos que, en tanto tales, se acoplan al campo magnético como si fueran pequeños imanes. Esto ofrece una manera sencilla de medir el denominado “momento magnético” del electrón; es decir, el factor que da cuenta de cuánto se acoplan esos pequeños imanes puntuales que llamamos electrones a un campo magnético externo. La manera de medirlo es la siguiente: si uno dispone un electrón en presencia de un campo magnético externo, el influjo de este último hará que el electrón, en tanto pequeño dipolo magnético, adquiera un movimiento de precesión en torno a la dirección en la que el campo apunta. La velocidad de ese giro resulta ser proporcional al acoplamiento con el campo magnético externo. Así, la medición de esa frecuencia de precesión permite obtener de manera directa el momento magnético, que suele denotarse factor-g, o simplemente g.

El factor-g del electrón, decíamos, no es sino la propensión que esta partícula tiene a interactuar con el campo magnético en el que se encontrara embebida. Este campo externo puede estar dado por el núcleo atómico en torno al cual el electrón se encuentra orbitando, o dado por otro electrón compañero, o por un arreglo experimental que se hubiere montado. En todos esos casos, el acoplamiento entre el electrón y el campo magnético en el que éste se encuentra inmerso está dado por el mismo factor-g.

Fue muy al comienzo de la física de partículas cuando se advirtió que el valor del factor-g para un electrón parecía ser g = 2; un valor peculiar ya que si se pensaba al electrón clásicamente era esperable un factor diferente. No obstante, ya a comienzos de la década del 30 se entendía la razón del valor 2 para el factor-g electrónico; la ecuación de Dirac, que es la ecuación que describe el campo cuyas excitaciones llamamos “electrón”, predice exactamente ese valor, g = 2. En efecto, la explicación de ese valor es uno de los grandes primeros logros de la teoría cuántica relativista.

El vacío cuántico

Ahora bien, los datos experimentales de la medición del factor-g llegarían unos años más tarde: En 1948, Kusch y Foley midieron por primera vez el factor-g, obteniendo como resultado el valor g = 2,00232, ligeramente superior al límpido 2 predicho por la teoría. Esta discrepancia con el valor g = 2 es lo que se conoce como “momento magnético anómalo”, y es la razón por la cual uno refiere a la cantidad g-2 como la verdaderamente relevante.

Esta discrepancia entre el valor g = 2,00232 y el valor g = 2, sin embargo, se entendió al poco tiempo. Fue Schwinger quien propuso la explicación correcta de por qué el valor experimental obtenido para g no era 2 sino un valor ligeramente mayor. La razón es la mecánica cuántica: según la teoría cuántica, lo que conocemos como vacío es algo muy diferente al concepto clásico que tenemos de él. El vacío no es la ausencia total de materia y energía en una región del espacio. La teoría cuántica de campos nos enseña que, de hecho, el vacío no es la nada sino algo muy diferente: Es un constante fluctuar de partículas y antipartículas que se crean y aniquilan incesantemente, dando origen a una estructura efervescente que, por consiguiente, denominamos “vacío cuántico”. Así, la mera presencia de una partícula en el espacio, por caso un electrón o un muón, genera en torno a sí una polarización de ese vacío cuántico, y la partícula termina vistiéndose de un halo fluctuante de partículas y antipartículas virtuales arrancadas a la nada.

Podemos entender esta poiesis cuántica de partículas virtuales y cómo ésta afecta al comportamiento de un electrón en presencia de un campo externo de la siguiente manera: en la teoría cuántica de campos, la interacción de un electrón y el campo magnético externo se describe en términos del intercambio de partículas. La interacción electromagnética está mediada por un fotón, y ese fotón colisiona con el electrón afectando su comportamiento. Mientras que la visión macroscópica que tenemos del fenómeno es la de un electrón exhibiendo un movimiento de precesión debido al influjo de un campo magnético externo, la visión microscópica del mismo fenómeno nos devela que es la colisión entre el electrón y uno de los fotones que conforman el campo magnético lo que acaece (ver Figura 1-A). Al interactuar con el fotón, el electrón reacciona de la manera observada. Ahora bien, debido a la fluctuante naturaleza del vacío cuántico, el electrón tiene permitido efectuar muchas más peripecias que el mero interactuar con el fotón. Por ejemplo, antes de hacer esto último, el electrón pudo haber elegido emitir su propio fotón virtual, luego impactar con aquel que le trae la información del campo magnético externo, y finalmente reabsorber el fotón virtual originalmente emitido (Figura 1-B). Pero hay más: como si se tratara de un malabarista que encuentra desafiante poner más bolas en el aire, el electrón puede generar, no sólo uno, sino dos, tres o más fotones virtuales y, luego de impactar con aquel que le trae la información del campo magnético externo, reabsorberlos (Figura 1-C). Puede hacer todo eso y muchas cosas más, muchas otras piruetas cuánticas, cada una de ellas con cierta probabilidad de realización. El resultado, entonces, se obtiene luego de sumar sobre todas esas peripecias, sobre todas esas historias; mientras que el resultado clásico g = 2 sólo corresponde a tener en cuenta el impacto directo entre electrón y el fotón (Figura 1-A). En otras palabras y tal como explicaba Schwinger, el resultado experimental para g será un poco mayor que 2 debido a que el electrón tiene a su disposición la creación de pares de partículas y antipartículas virtuales que terminan vistiendo el valor clásico g = 2 de otras posibles historias en ese interactuar, modificando así el valor del momento magnético ligeramente.

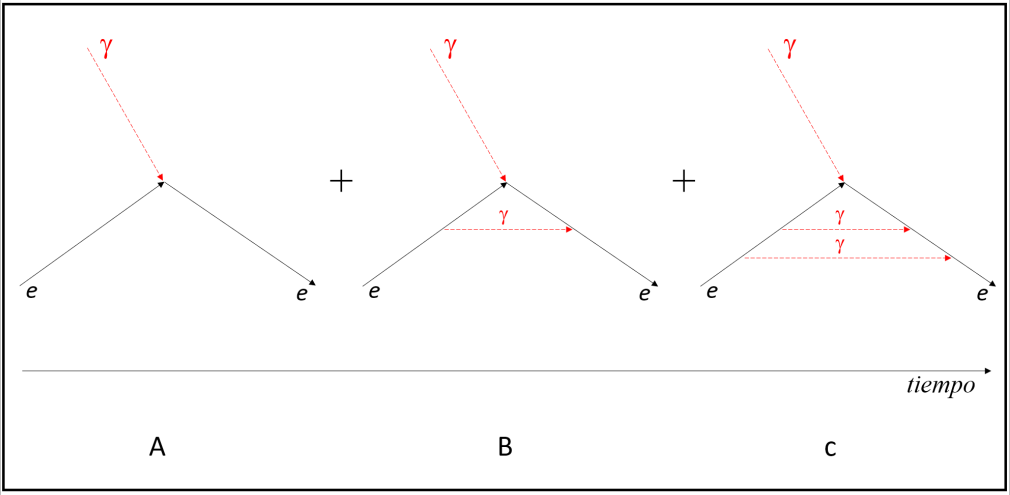
Los cálculos teóricos sobre todas las posibles contribuciones de pares de partículas y antipartículas en la interacción entre el electrón y el campo magnético externo arrojan una predicción al valor de g extremadamente precisa, con más de una decena de cifras significativas de exactitud. El hecho de que los resultados experimentales para el factor-g del electrón concuerden con los cálculos teóricos a semejante orden de precisión se yergue, hoy, como el resultado más preciso de toda disciplina científica.

El momento magnético del muón

Ahora bien, ¿ocurre lo mismo con el muón? Siendo que el muón y el electrón son dos partículas que, junto al tauón, coinciden en todas sus propiedades con excepción de la masa, ¿no debería, acaso, el resultado del momento magnético del muón arrojar resultados con precisión semejante a la obtenida para el caso del electrón? Pues, la historia no es tan sencilla: al ser el muón unas doscientos veces más masivo que el electrón, ése es mucho más propenso que este último a interactuar con partículas de gran masa. Típicamente, el acoplamiento de una partícula es proporcional al cuadrado de su masa, de manera tal que, al ser 200 veces más masivo que el electrón, el muón resulta ser unas 40.000 veces más susceptible a la interacción con las partículas virtuales. Esto requiere, en particular, mucho más detalle en el cálculo de las distintas contribuciones al acoplamiento entre el muón y el fotón. Al disponer un muón en un campo magnético externo, el muón, al igual que un electrón lo haría, comenzará a experimentar una precesión en torno a su eje de giro. Esa interacción entre el campo magnético externo y el muón se describirá, también como en el caso del electrón, en términos de intercambios de partículas, incluyendo las peripecias cuánticas que involucran partículas virtuales: al interactuar con el fotón portador del campo magnético externo, el muón puede colisionar directamente, pero puede también generar partículas virtuales antes de hacerlo y reabsorberlas luego de ello; puede generar fotones virtuales, partículas Z virtuales, e incluso generar partículas de Higgs virtuales, entre muchas otras cosas. El resultado teórico correspondería, pues, a sumar sobre todas esas posibilidades.

Ese cálculo, aunque la teoría para llevarlo a cabo es bien conocida y, por ello, no presupone mayor desarrollo teórico, sí requiere de paciencia y de una notable pericia a la hora de emplear las técnicas de cálculo. Es un cómputo extremadamente sensible a errores y a omisiones. Una tarea minuciosa es necesaria a la hora de tener “todas” las configuraciones intermedias en cuenta y con su adecuado “peso”. La comunidad especializada ha llegado a un “resultado de consenso” acerca del cálculo teórico para el factor-g del muón; a saber: g = 2,0023318319.

Ahora sólo quedaría cotejar con el experimento.

Los experimentos

El momento magnético del muón se midió por primera vez a comienzos de la década del 50 en la Universidad de Columbia, y una década más tarde el CERN arrojaba resultados en concordancia. El advenimiento de mejoras tecnológicas y nuevas técnicas experimentales permitieron un aumento significativo en la precisión, y hacia la década de 1990 los nuevos experimentos con los que hoy contamos estaban ya siendo diseñados. En 2001, el Laboratorio Nacional de Brookhaven, en los Estados Unidos, daba a conocer el valor medido experimentalmente para el factor-g del muón; éste era: g = 2,0023318404.

Como vemos, el valor experimental para g-2 difiere del teórico en la novena cifra significativa, lo que podría hacernos creer que se trata de un éxito de la teoría. Pero lo cierto es que no es así: se trata de una medición muy precisa, por lo que los errores en la medición son extremadamente pequeños, lo suficiente como para considerar que se trata de un desacuerdo.

A partir de 2013, partes del experimento de Brookhaven se trasladaron al Fermilab, en Chicago, donde se montó un arreglo similar pero con notables mejoras. Funciona allí la colaboración Muon g-2, que realiza el experimento más preciso hasta el momento para medir el factor-g del muón. El experimento consiste en un anillo de unos 15 metros de perímetro en el que se aceleran muones a muy altas velocidades. Luego de ser inyectados en el anillo, los muones giran mientras se los somete a un campo magnético externo de intensidad muy controlada. Debido al campo magnético, los muones experimentan el mentado movimiento de precesión cuya frecuencia es medida con la precisión requerida.

El pasado 7 de abril, en conferencia de prensa, la colaboración trabajando en el experimento Muon g-2 dio a conocer sus resultados, que vienen a confirmar la discrepancia entre el valor para el factor-g medido experimentalmente y la predicción teórica basada en el Modelo Estándar. En otras palabras, los resultados de Muon g-2 resultan ser consistentes con los experimentos de Brookhaven, exhibiendo, cuando se los considera en conjunto, una tensión de unas 4,2 sigmas de desviación estándar con respecto al valor teórico.

Esto nos enfrenta a una discrepancia entre teoría y experimento, ahora corroborada y medida con mayor precisión. Surge así la pregunta: ¿Estamos ante el descubrimiento de una grieta en el edificio teórico que llamamos Modelo Estándar de partículas fundamentales? ¿Estamos ante lo que los físicos de partículas llaman “nueva física”? La verdad es que no lo sabemos con certeza.

Hay, al menos, tres posibles explicaciones para la discrepancia observada: una posibilidad es que ésta se deba a una fluctuación estadística. Que los datos de las corridas del experimento analizadas hasta la fecha arrojen como resultado una discrepancia con el valor teórico de consenso a 4,2 sigmas hace que este sea un caso serio contra la teoría que tenemos; pero en física de partículas, dada la enorme exactitud que se ha alcanzado en los experimentos y dada la gran dependencia de los resultados con la estadística, la convención es que un descubrimiento se considera tal sólo cuando se han alcanzado los 5 sigmas de desviación, y para ello hace falta seguir analizando los resultados que la colaboración Muon g-2 ha tomado en los últimos años.

La segunda posible explicación para la discrepancia es que a la hora de efectuar los cálculos teóricos se hayan subestimado las contribuciones de partículas virtuales a la hora de pensar todas las formas en las que el muón puede interactuar con el campo magnético externo. Al tener una masa considerable, el muón es también propenso a emitir partículas virtuales que no son solamente partículas elementales, sino también hadrones. Los hadrones son estados ligados que están, a su vez, formados de muchas otras partículas que interactúan mediante la fuerza nuclear fuerte. Esos estados están descriptos por la teoría llamada cromodinámica cuántica en un régimen en la que la misma es difícil de domeñar. Ejemplos de hadrones son el pión y el kaón, formados éstos por un par quark-antiquark embebido en un orgiástico menjunje de gluones y acompañado con una fluctuante maraña de pares de quarks-antiquarks virtuales que se crean y aniquilan incesantemente. ¡Algo muy complejo! La consideración de la posibilidad de que el muón, antes de interactuar con el fotón del campo magnético externo, emita y luego reabsorba uno de estos hadrones complica mucho el cálculo teórico, ya que los hadrones tienen, per se, una complicada estructura interna. Y aunque la física de hadrones es en alguna medida conocida y contamos con datos experimentales para extrapolar resultados, ponderar su contribución es, sin lugar a dudas, la parte más abstrusa del cálculo. En el caso del electrón esto no representaba un inconveniente, ya que el electrón, debido a su baja masa (0,51 MeV), no tiene alta propensión a este tipo de interacciones; pero sí es menester tenerlas en cuenta en el caso del muón.

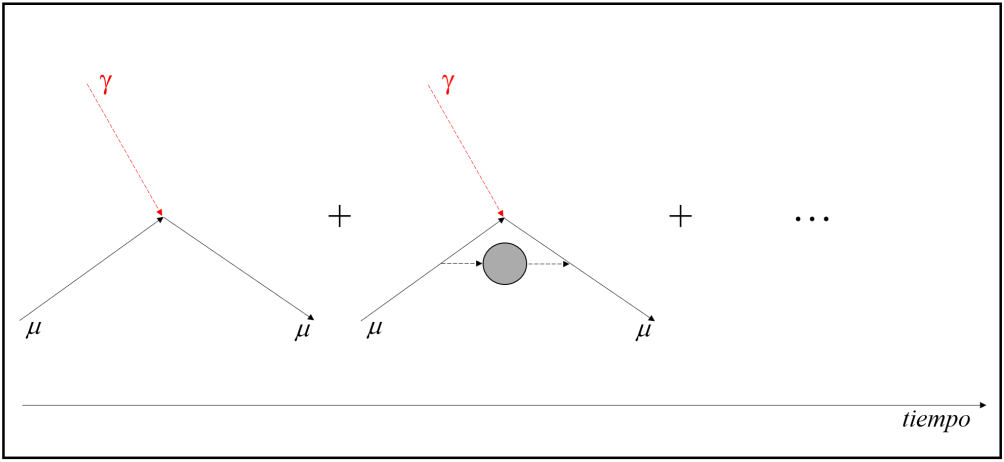
La tercera posible explicación, y la que se anuncia con más acento debido a las posibles implicancias que ésta tendría para la física, es que el Modelo Estándar no sea un modelo completo; es decir, que deba el Modelo ser completado con la adición de partículas que aún no conocemos. Podría estar ocurriendo que el muón, en su interactuar con el fotón del campo magnético externo, estuviera generando otras partículas virtuales cuya existencia desconocemos pero de las que el muón sí se entera. La posibilidad de que el muón pueda emitir y luego reabsorber una partícula tal, además de hacerlo con las que ya conocemos, aumentaría el valor de g acercándolo al valor experimental observado. Así, sugieren algunos, podríamos estar observando indirectamente la presencia de esas partículas nuevas, desconocidas, nuevas partículas fundamentales que deberíamos agregar a nuestro Modelo; en breve, podríamos estar frente a lo que los físicos de partículas insisten con llamar “nueva física”.

Tenemos por delante una década de refinamiento de los cálculos teóricos, de mejoras en las técnicas de observación, y de recopilación de más datos estadísticos. El tiempo nos sabrá decir cuál es la explicación a la sutil discrepancia entre el valor teorizado y el valor observado para el factor-g del muón. Pero, insisto, seamos cautelosos; no sería la primera vez que el Modelo Estándar saliese victorioso luego de haber sido desafiado, y aunque la precisión alcanzada en el experimento Muon g-2 es asombrosa, es necesario esperar.