Flujo intermitente de sistemas particulados y transición de atasco

Paula Gago. Facultad Regional La Plata. Universidad Tecnológica Nacional y CONICET.

¿Existen similitudes en el comportamiento de la sal en un salero, ovejas saliendo del establo a pastar y un grupo de personas abandonando un edificio? Intentaré convencerlos de que sí, contando algunas de las similitudes que se han encontrado recientemente en un trabajo conjunto que realizamos con colegas de la Universidad Tecnológica Nacional, el Instituto Tecnológico Buenos Aires, la Universidad de Navarra, la Universidad de Edimburgo, la Universidad de Zaragoza, la Escuela Superior de Física y Química Industrial de París y la Universidad de Barcelona.

La primera similitud que podemos sugerir es que todos estos sistemas (junto con una gran variedad de otros) pertenecen a la categoría de sistemas particulados; esto es, son un conjunto numeroso de elementos de tamaño macroscópico (que se aprecian a simple vista) que interactúan entre ellos. Pensemos por ejemplo en los diferentes recorridos que atraviesa una persona caminando por una calle vacía o por una calle repleta de otras personas. En el primer caso el recorrido típico será en línea recta, del lugar donde se encuentra al lugar a donde desea dirigirse, en el segundo caso será necesario realizar un camino zigzagueante que permita evitar el contacto con los demás peatones.

En la definición dada de sistema particulado no nos interesará entonces el comportamiento individual de cada elemento, sino el comportamiento del conjunto, causado por las interacciones presentes. Si aceptamos esta primera similitud podemos avanzar a la que nos convoca, el flujo de estos sistemas particulados a través de orificios o aberturas angostas.

Un salero que se tapa

Podemos decir que los sistemas particulados poseen la capacidad de "fluir" a través de un orificio o abertura, tal como lo hace la arena del reloj de arena, o la gente a la salida del cine. Para esto necesita algún tipo de fuerza impulsora (en el caso de la arena la gravedad, en el caso de las personas alguna motivación). En estos casos el sistema se comporta como una especie de fluido que puede adaptarse a la forma de la abertura y a la situación (es decir, intentar moverse más rápido o más lento dependiendo de la fuerza o motivación).

Sin embargo, un salero que se tapa es un fenómeno de todos los días y esta es otra propiedad que tienen en común los sistemas particulados. Si prestamos atención veremos que el flujo de personas saliendo del cine no es continuo ni homogéneo. Presenta interrupciones de diferente duración sólo que aquí, a diferencia de lo que ocurre con la sal, las mismas "partículas/personas" son las que se encargan, mediante tirones y empujones, de destrabar el embotellamiento y seguir saliendo. En el caso del salero, como bien sabemos, resulta necesario sacudirlo o golpearlo un poco para obtener el mismo efecto de reanudación del flujo.

Al aplicar algún mecanismo para reactivar el flujo de estos sistemas se obtiene lo que se llama un flujo intermitente de sistemas particulados. En estos casos el tiempo que le tomará al sistema reanudar el flujo una vez producido el atasco dependerá de muchos factores: la humedad de la sal, el tamaño del orificio del salero, la fuerza que impulsa al sistema a fluir, etc; así como del mecanismo de desbloqueo aplicado.

Para muchos fines prácticos, conocer el tiempo que lleva restablecer estos flujos tiene gran importancia. Para esto, lo que haríamos generalmente sería repetir varias veces el "experimento" midiendo el tiempo de desatasco en cada caso y después promediando estos tiempos obtendríamos una estimación del tiempo característico de atascamiento. Sin embargo, este método de promediado sólo es válido para algunos fenómenos, en el problema que nos convoca no lo es.

Este problema de flujo intermitente en sistemas particulados requiere de un análisis diferente. Tratemos de entender porqué.

Las leyes de probabilidad

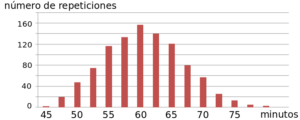
Cuando queremos dar información sobre un hecho repetitivo (el tiempo que tarda el tren en ir de A a B por ejemplo) hablamos de forma intuitiva del promedio de estos valores sobre el número total de medidas realizadas (el número de veces que viajamos). No nos importa cuanto tardó ayer ni cuanto tardó hoy; no queremos el detalle del tiempo de cada viaje, queremos información general, una cantidad que nos sirva para predecir de un modo aceptable la duración de los viajes siguientes. En la figura de la izquierda podemos ver un ejemplo de lo que se llama una ley de probabilidad "normal".

Supongamos que viajamos 1000 veces de A a B. Cada linea en la figura representa la cantidad de veces que el tren tardó 40, 45, 50, 55, etc minutos en el trayecto. Claramente, la mayoría de las veces, aproximadamente 160, el tren tarda una hora, aunque puede tardar unos minutos más o unos minutos menos (seguramente dependiendo del tránsito). Según este experimento, con gran probabilidad llegaremos a destino a tiempo si tomamos el tren una hora antes. Este tipo de distribución también se distingue por ser simétrica, es decir que podemos con igual probabilidad llegar 5 minutos antes o cinco minutos después y el promedio o media coincide con el tiempo que se repitió la mayor cantidad de veces, llamado moda. Las distribuciones normales ocupan un lugar importante en el estudio probabilístico de algunos fenómenos de la naturaleza, es por esto que sus propiedades (es decir, las propiedades de las cantidades que poseen este tipo de distribución) han sido intensamente estudiadas.

Flujo intermitente de sistemas granulados

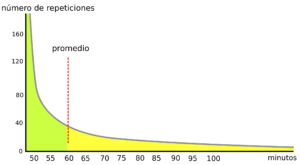
Si miramos ahora la distribución que resulta de medir los tiempos de duración de los atascos en el flujo intermitente de los sistemas particulados veremos que esta distribución no resulta del tipo normal sino que tiene la forma mostrada en la figura de la derecha. En esta puede apreciarse que existe una alta probabilidad asociada a tiempos cortos pero que también existe probabilidad, aunque cada vez menor, de tener atascos de muy larga duración.

En esta figura la línea de trazo en rojo marca el valor correspondiente al promedio de los tiempos obtenidos. Podemos ver que en este caso esta cantidad no nos provee mayor información de lo que pasa en el sistema. No nos permite predecir, ya que la mayoría de las veces los atascos se romperán rápidamente, pero existe una probabilidad de que duren mucho tiempo más de lo que indica el promedio.

En el caso de estar interesados, por ejemplo, en predecir de forma aceptable el tiempo que lleva evacuar determinado edificio será necesario entonces intentar un nuevo enfoque. Construyamos entonces las llamadas distribuciones acumuladas, que en este caso significa simplemente "la probabilidad de que la duración de un atasco sea mayor que". Es decir, no el número de veces que un atasco duró 3, 5 o 7 minutos, sino el número de atascos que duraron más de 3, más de 5 o más de 7 minutos. En la figura de abajo podemos ver el resultado de tomar la distribución acumulada para los tiempos de atascos correspondiente a la descarga de un silo con granos que posee una abertura pequeña y se vibra constantemente para romper los atascos que se forman durante el flujo.

En esta figura las dos curvas representadas corresponden a dos fuerzas de gravedad efectiva distintas con las que las partículas son empujadas a moverse a través del orificio de salida del silo. Esto se consigue cambiando la inclinación del silo con respecto a la vertical. Podemos ver que para la curva roja, la probabilidad de tener atascos largos es mayor que para la curva azul, correspondiente a una aceleración mayor. Este es un fenómeno interesante, que sin embargo no voy a poder contar en esta nota.

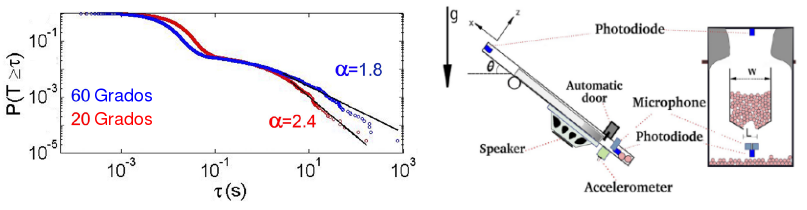
Los datos de este gráfico se encuentran representados en una escala llamada escala logarítmica y así representados puede verse que en la región de tiempos largos estas gráficas se asemejan a una linea recta. Este tipo de comportamiento puede describirse matemáticamente mediante lo que se conoce como una ley de potencias: $$P(T > τ) = τ^{(-α)}$$ Sin entrar en detalles, lo que quiero es remarcar la importancia del parámetro α en esta ecuación. El valor de α será diferente para las distintas curvas en el gráfico y nos indica que tan rápido o lento decrece la probabilidad de tener tiempos de atascos largos. Por ejemplo, para la evacuación de un edificio, querríamos conseguir un exponente α lo mayor posible, lo que aseguraría muy baja probabilidad de tiempos de atasco, y por consiguiente tiempos de evacuación, largos.

Sin embargo, ¿cuál sería el valor mínimo aceptable o el valor óptimo en cada caso? Esto es algo que no puede definirse de forma simple y necesita de un estudio más profundo a partir de las situaciones específicas. Lo que si podemos decir es que estas distribuciones presentan características completamente diferentes para valores de α por encima y por debajo de 2. En la mayoría de los casos queremos asegurar un valor α > 2.

Transición de "atasco"

El tipo de función matemática propuesta para los tiempos de atasco tiene la particularidad de que para un valor de α mayor que 2, luego de realizar un número suficientemente grande de repeticiones (suficientemente grande dependiendo del caso puede se 100, 1000, 10000 o más), el valor promedio de la distribución no variará significativamente con las repeticiones subsiguientes. Sin embargo, valores α menores que 2 implican que el valor promedio que obtendremos si realizamos repetidamente este experimento (por ejemplo la descarga de un silo o salero) no será el mismo si repetimos el experimento 100, 1000 o 10000 de veces, dependerá de las repeticiones realizadas y su valor puede cambiar de forma radical entre la medida número 10000 y la 10001!

En la figura vemos que para los tiempos de atasco de un silo bidimensional es posible que el valor del parámetro α tome valores por debajo y por encima del valor crítico 2, tan solo cambiando la fuerza que impulsa a las partículas hacia la salida. Este fenómeno, que ha sido observado también en el flujo intermitente de otros sistemas partículados, como un rebaño de ovejas o en la evacuación de personas (este último estudiado mediante modelos de simulación por computadora) ha sido llamado transición de atasco (clogging transition).

Las transiciones son saltos bruscos de las propiedades de los sistemas al variar levemente algún parámetro de control. En el caso del agua hirviendo, por ejemplo, la densidad cambia de forma brusca de líquido a vapor, mientras que la temperatura del sistema sólo necesita cambiar de digamos 99C a 101C. En el caso que nos ocupa es posible, variando características propias del sistema estudiado (ancho del orificio de descarga o puerta, aceleración del sistema, urgencia por salir, etc), que el exponente α tome valores por encima y por debajo del 2. Por lo tanto, los tiempos medios de evacuación pasarían de estar bien definidos luego de un número suficientemente grande de medidas, a seguir teniendo la capacidad de variar siempre que agreguemos más medidas al experimento.

Entonces...

Existen similitudes entre la descarga de un silo o el comportamiento de la gente a la salida de un estadio. Entre estas similitudes pudimos ver que el flujo intermitente presenta, para los tiempos de atasco, una transición de fase conocida como transición de atasco. Este tipo de resultado tiene uno de sus mayores puntos de interés en la nueva perspectiva que ofrece al estudio de las normas de seguridad para evacuación peatonal, donde resulta fundamental tener la mayor precisión posible en los tiempos que el proceso lleva.

También resulta útil a la hora de analizar procesos productivos, donde los materiales particulados son ampliamente manipulados y suelen encontrarse con la necesidad de lidiar con este tipo de atascos. Pero además de sus aplicaciones técnicas, desde un punto de vista científico, la existencia de una transición de fase en este tipo de sistemas ofrece un amplio e interesante campo de investigación. Las transiciones de fase y los saltos bruscos y discontinuidades que implican, siempre han resultado fascinantes para quienes estudian la naturaleza y quieren intentar comprender el cómo y del porqué de estas discontinuidades.

La existencia de esta transición en flujos intermitentes de sistemas particulados con características tan variadas hacen que su estudio y generalización resulten atrayentes para intentar dilucidar los fenómenos que subyacen a la naturaleza de los mismos.

Trabajo original: I. Zuriguel, D. R. Parisi, R. Cruz Hidalgo, C. Lozano, A. Janda, P. A. Gago, J. P. Peralta, L. M. Ferrer, L. A. Pugnaloni, E. Clement, D. Maza, I. Pagonabarraga, A. Garcimartin, Clogging transition of many-particle systems flowing through bottlenecks, Scientific Reports 4, 7324 (2014)

Contacto: Paula Gago ([email protected])