¿De dónde vienen las oscilaciones epidémicas?
Guillermo Abramson. Grupo de Física Estadística e Interdisciplinaria del Centro Atómico Bariloche, CONICET e Instituto Balseiro.
Desde épocas remotas las epidemias han causado enorme sufrimiento a la Humanidad. Cada civilización sobrellevó sus plagas de la mejor manera que pudo, y éstas fueron forjando en alguna medida el curso de la Historia. Hasta hace no muchas décadas las enfermedades infecciosas tenían una presencia en la vida cotidiana mucho mayor que hoy en día. Esto era así aún en las regiones más favorecidas del mundo. La malaria, la difteria, la sífilis, la meningitis meningocóccica, y mucha, mucha tuberculosis. Gracias a los avances en áreas que van desde los antibióticos a la plomería (y sobre todo a mucho dinero) gran parte de estas pestes ya casi no existen en las regiones más desarrolladas, así como en buena parte del mundo subdesarrollado. Cada tanto, sin embargo, la sombra de una vieja o de una nueva plaga aparece en el horizonte.
Ronald Ross (nacido en Almora, India, en 1857) fue un médico genial, descubridor del agente causante de la malaria y de su transmisión por el mosquito, por lo cual recibió el Premio Nobel de Medicina en 1902. Era aficionado a la matemática, y publicó en 1917 un artículo [1] en el que manifiesta su asombro de que no existiera una teoría matemática de la propagación de epidemias, un campo en el cual se tenían, desde hacía tiempo, grandes cantidades de datos estadísticos esperando ser examinados. Dice, además, que las cuestiones fundamentales de la epidemiología, en las cuales se basan las medidas preventivas (tales como la tasa de contagio, la frecuencia de brotes o la pérdida de la inmunidad) no pueden ser resueltas por métodos que no sean analíticos. ¿A qué se debe que algunas enfermedades persistan en la población, mientras que otras aparecen y desaparecen? ¿Por qué existen las epidemias? Ross sospechaba que la respuesta a estas preguntas se esconde en principios fundamentales a los que puede accederse mediante el cálculo, del mismo modo que en la Astronomía, la Física y la Mecánica.
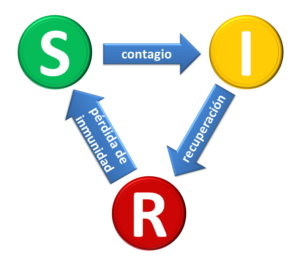
El campo interdisciplinario del estudio matemático de las epidemias se ha desarrollado considerablemente en el siglo transcurrido desde la propuesta pionera de Ross, pero queda sin embargo mucho por hacer. Los modelos tradicionales están basados en la división de la población en categorías, de acuerdo a su estado infeccioso. Poco después de Ross un par de científicos escoceses, William Kermack (químico) y Anderson McKendrick (médico) propusieron el que se ha convertido en el padre de todos los modelos epidemiológicos: el modelo SIR [2]. Los individuos que componen la población pertenecen a las categorías susceptibles (S), infectados (e infecciosos, I) o recuperados (e inmunes, R). Existen transiciones entre estos estados, controladas por fenómenos tanto epidemiológicos como sociales. Los susceptibles pueden contagiarse por contacto con infectados, pasando del estado S al I. A su vez los infectados se recuperan, pasando al estado R. El balance entre la velocidad a la cual ocurren estos dos procesos determina la evolución de la epidemia. Usualmente se condensa esto en términos de un único parámetro, la tasa reproductiva de la infección, que expresa el número de infecciones secundarias producidas por cada caso de la enfermedad. Si este número es mayor que 1, entonces ocurre una epidemia. Si es menor que 1, el “brote” inicial decae. A medida que la infección se va propagando la cantidad de susceptibles disminuye, de manera que a la infección se le hace cada vez más difícil propagarse, eventualmente empieza a decaer, y finalmente se extingue.
Es fácil ver que este modelo sencillo es una caricatura de lo que ocurre en la realidad. Por un lado, la historia natural de muchos agentes infecciosos es más complicada. Pueden existir estados latentes (infectados pero no infecciosos), una respuesta inmune compleja (inclusive dependiente de la edad del anfitrión), pérdida de la inmunidad (con regreso de los R al estado I), vacunación y tratamientos, una demografía con nacimientos, muertes y migraciones, y un largo etcétera. Por otro lado, existen hipótesis más sutiles en la formulación matemática de estos sistemas, cuya modificación podría producir un comportamiento dinámico distinto. En nuestro trabajo hemos estudiado estos problemas desde numerosos puntos de vista [[3](#3 "3·), - 6 "6"], tratando de dilucidar el rol de los distintos mecanismos que se esconden detrás de esas hipótesis. Por ejemplo, ¿qué ocurre si la población, en lugar de estar bien mezclada, con contactos de "todos con todos", está organizada en una red social, como ocurre en la realidad? [3]. ¿Y qué pasa si, en lugar de analizar poblaciones grandes que evolucionan de manera suave, la población es pequeña y las fluctuaciones que ocurren a nivel individual son relevantes? [4]. O, por otro lado, ¿qué pasa si los fenómenos infecciosos no ocurren a tasas constantes como se supone habitualmente, sino que deben cumplir plazos más o menos bien definidos? En los próximos párrafos veremos con algún detalle este último caso, que es el objeto de nuestros trabajos más recientes [5,6].
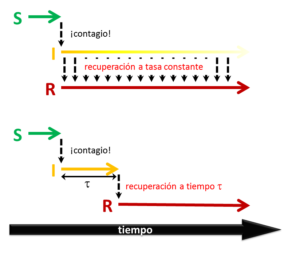
¿Qué significa que los fenómenos infecciosos ocurren a tasas constantes? Pensemos en lo que ocurre al individuo apenas contagiado en un modelo SIRS (es decir, con pérdida de la inmunidad). Acaba de ingresar a la categoría I, en la que permanecerá hasta que se recupere. Una tasa constante de recuperación significa que el individuo tiene una cierta probabilidad de curarse hoy, la misma probabilidad de curarse mañana, la misma probabilidad de curarse pasado mañana... ¡y así sucesivamente hasta que se cure! Esto, claramente, está lejos de la realidad para muchas enfermedades infecciosas. Es mucho más razonable suponer que, lo que ocurrirá, es que el infectado se recuperará una vez transcurrido cierto tiempo característico de su enfermedad. A lo sumo un poquito antes, o un poquito después. Lo mismo puede decirse de la duración de la inmunidad en el estado R. Estos mecanismos de recuperación y de pérdida de la inmunidad con tiempos característicos pueden también formularse matemáticamente. El análisis es un poco más complicado, razón por la cual no se lo usa habitualmente. En [5] hemos analizado un sistema SIRS de este tipo, en situaciones en las que el análisis "clásico" (al estilo de Kermack y McKendrick) predice un comportamiento de tipo endémico, con una pequeña fracción de la población que permanece infectada. Encontramos que la hipótesis de tiempos característicos de recuperación y pérdida de inmunidad, en cambio, produce una dinámica oscilatoria, con rebrotes periódicos de la infección. La aparición de las oscilaciones depende de dos factores. Por un lado, el tiempo de pérdida de la inmunidad debe ser mayor que el de recuperación (cuánto mayor depende, además, de la tasa reproductiva). Parece un resultado inocente, pero puede ser muy relevante en la vida real. Imaginemos que estamos ante un agente infeccioso endémico en una población, con una cierta prevalencia. Ahora imaginemos que el tiempo de inmunidad se alarga, por ejemplo por mejoras en una vacuna. Podemos empezar a ver una oscilación, ¡inclusive con aumento de la prevalencia! Eso no significa que la vacuna no esté funcionando, claro está, ya que el valor medio de la prevalencia puede disminuir. Evidentemente es algo que hay que tener en cuenta.
Por otro lado, como dijimos antes, los tiempos de infección y de inmunidad pueden no ser exactos, sino más o menos difusos alrededor de un valor medio. El modelo predice que, para que aparezcan las oscilaciones, ninguno de estos procesos puede estar muy desparramado alrededor de su valor medio. Existe un ancho crítico, por debajo del cual las recuperaciones y las pérdidas de inmunidad de los distintos individuos "no se mezclan". Esto permite la sincronización de la infección en muchos de ellos, condición necesaria para la oscilación. En ambos casos se trata de una transición en el comportamiento dinámico de la epidemia en función de la historia natural del agente infeccioso, en lugar de depender de la tasa reproductiva que controla los modelos clásicos.
Muy bien, tenemos un modelo matemático de epidemias que produce oscilaciones. ¿Existen las oscilaciones epidémicas en el mundo real? Claro que sí. El sarampión, antes de la introducción de la vacunación masiva a fines de los '60, rebrotaba cada dos años en muchos países. La tos convulsa, una infección para la cual también existe vacuna pero que está reapareciendo, oscila con un período de 4 años. Se ha evidenciado un período de 11 años en los brotes de sífilis en algunas ciudades norteamericanas. Varias enfermedades respiratorias, muy ligadas a la estacionalidad anual, oscilan sin embargo con período bienal. Es el caso de la parainfluenza de tipos 1 y 3, y de la propia gripe, que parece tener picos en distintas semanas en años pares o impares en algunas ciudades. Nuestro modelo predice períodos de oscilación que son compatibles con los parámetros epidemiológicos de varias de estas enfermedades. En particular, cuando se supone adicionalmente que la tasa de contagio está sujeta a oscilaciones estacionales (como en el caso de las enfermedades tipo influenza), observamos 6 oscilaciones con dos picos anuales, pero que ocurren en momentos distintos del año, tal como se observa en situaciones reales.
Podemos concluir, por un lado, que es posible formular modelos matemáticos que relajen las hipótesis fuertes que hacen que, muchas veces, los modelos clásicos de enfermedades infecciosas parezcan caricaturas de la realidad. Por otro lado, que existen fenómenos dinámicos novedosos cuando estudiamos cada una de estas suposiciones por separado. Finalmente, que estos modelos se caracterizan por un fenómeno de sincronización de la fase infecciosa, que se manifiesta en la aparición de oscilaciones de distinta complejidad, cuyas propiedades pueden estudiarse detalladamente. Existen muchos mecanismos por los cuales un sistema epidémico puede manifestar oscilaciones. Ciertamente, en la naturaleza pueden operar simultáneamente más de uno, de manera que es necesario estudiar cuidadosamente sus características e interacciones.
Para saber más:
El artículo de Wikipedia sobre el modelo SIR está muy bien (en inglés). Si quiere explorar su dinámica, hay un simulador on line en la Universidad de Bayreuth. El episodio 3 de la primera temporada de la serie televisiva NUMB3ERS trata sobre los modelos SIR. Visite la página web del autor y la del Grupo de Física Estadística e Interdisciplinaria. Y si le gusta la astronomía, no el blog del autor: En el cielo las estrellas.
Referencias
1. Ronald Ross, An application of the theory of probabilities to the study of a priori Pathometry, Proc. Roy. Soc. Lond. 93A, 225–240 (1917).
2. William Kermack and Anderson McKendrick, A contribution to the mathematical theory of epidemics, Proc. Roy. Soc. Lond. 115A, 700–721 (1927).
3. Marcelo Kuperman and Guillermo Abramson, Small world effect in an epidemiological model, Phys. Rev. Lett. 86, 2909–2912 (2001).
4. Sebastián Risau-Gusman and Guillermo Abramson, Bounding the quality of stochastic oscillations in population, Eur. Phys. J. B 60 , 515–520 (2007).
5. Sebastián Gonçalves, Guillermo Abramson and Marcelo F. C. Gomes, Oscillations in SIRS model with distributed delays, Eur. Phys. J. B 81, 363–371 (2011).
6. Sebastián Gonçalves, Guillermo Abramson and Marcelo F. C. Gomes, The interaction between seasonality and delays in epidemic models, en preparación.